Counting
Basics
Combinations: Jack and Jill 2C2 = 1
Permutations: Jack and Jill or Jill and Jack 2P2 = 2, n choices then n-1...
Arrangements: n choices each time
- OR = +
- AND = *
- If a number or something is fixed we remove that from our choices.
Ordering 10 People
- 10! ways. (10 spots, 9 spots, 8spots…)
Arranging Letters
Arranging the letters in “DATABASES”
- 9 letters
- 3 As
- 2 S
Total ways = 9!/3!2! (divide the repeated letters)
Staircase Paths
Staircase paths from (2,1) to (7,4)
- 7-2=5
- 4-1=3
- 5 Rights and 3 Ups
Ways to arrange: 8!/3!5!
Circular Tables
Arranging people at a circular table.
- 6 people, 6 positions 6! ways to arrange
- Want to remove the ways which are rearrangements of already counted positions do we divide by the 6 positions.
Therefore total arrangements are 6!/6 = 5!
No Adjacent Letters
Consider the word: TALLAHASSEE
There are 11! ways to arrange the letters and dividing by repeats we get 11!/2!3!2!2!
if we don’t want adjacent A’s then we remove all the A’s to get:
Which is 8 letters and 8!/2!3!2! ways to arrange them. Then there are 9 positions in between the letters to place 3 A’s so we have 9C3 (we don’t have to divide by 3! for repeated A’s since it’s a combination and we’re not counting them.)
Then by rule of product there are 8!/2!2!3! * 9!/6!3! arrangements.
No Consecutive Items
Suppose you have 9 balls and 5 bins to put them in. However you do not want any two consecutive, how can we calculate this?
- For the first ball there are 5 options since all bins are empty.
- For the second ball there is now only 4 options because one of them has been taken.
- For the third ball there is also only 4 options because we cannot have consecutive balls so it cannot go into the bin that ball 2 went into.
This pattern is repeated and the solutions becomes 5*4^8.
At Least and At Most
At Least:
Ex 1. Consider that there are 13 people, 7 women and 6 men. We want to choose 5 out of the 13.
If we want to select at least 1 female then we can select 1 or morefemales (up to 5)
So we can take the total amount of ways to select 5 people out of 13 and subtract that by the number of ways to get no females and all males.
We do this because the inverse of at least 1 is 0.
- 13C5 - 7C0 * 6C5
At Most:
Ex 2. At most 3 males
This means we can have 0,1,2 or 3 males.
The opposite of this is 4 or more males.
Hence, we can take total amount of ways to choose 5 people and subtract the ways we can get 4 males of 5 males.
- 13C5 - 7C1*6C4 * 7C0*6C5
Arrangement of Teams
24 kids divided into 4 teams of 6, in how many ways?
Combinations With Repetition
- Formula: (n+r-1Cr)
Example:
- This is a combinations with repetition because if we select 1 donut of a kind then there are still 11 and we can select from that again.
- Can be written as x1 + x2 + x3 + x4…x12 = 20
- The solutions to this is (20+12-1C12)
- Think of this like 20 baskets and we want to place 12 things in them. where you can put 0-12 in each of them
- 🍩🍩🍩🍩🍩🍩|🍪🍪🍪|🍰🍰🍰|||||||||||||||||
- There are 6 donuts for the first basket (first flavor) 3 for the next flavor and 3 for the 3rd flavor. With a remaining 8 empty baskets which donuts could have been placed.
Integer Solutions
Solutions to: x1 + x2 + x3...x6 < 10
The total sum should be less than 10.
Let's assume the sum is 9.
- x1+x2+x3...x7 = 9
- and we can solve this as (7+9-1C9)
- 9 things and 7 containers. where 9=r and 7=n.
Identical and Non-identical Items
Example: 5 identical and 5 different, 10 total items, we want to choose 5 items.
We can choose from the set of identical or nonidentical. So for each of 5 items there are 2 choices.
Where n^r (n is the containers and r is the items)
Logic
Basics
Exclusive Or = either one is true but not both.
Biconditional = p->q <--> q->p p if and only if q, p is necessary and sufficient for q.
- If validating by truth table, when premises are true, the conclusion must be true.
- If assigning truth values, show that if the conclusion = 0 then the premises cannot = 1.
Ways to write implication p->q
- if p then q
- p is sufficient for q
- p implies q
- q only if p
- q if p
- q is necessary for p
p->q is true always except when p is 1 and q is 0.
Negating Implication
- P->Q
- ~PvQ
- ~(~PvQ)
- P^~Q
P but not Q. If writing in English don't include the word if.
Logic Laws
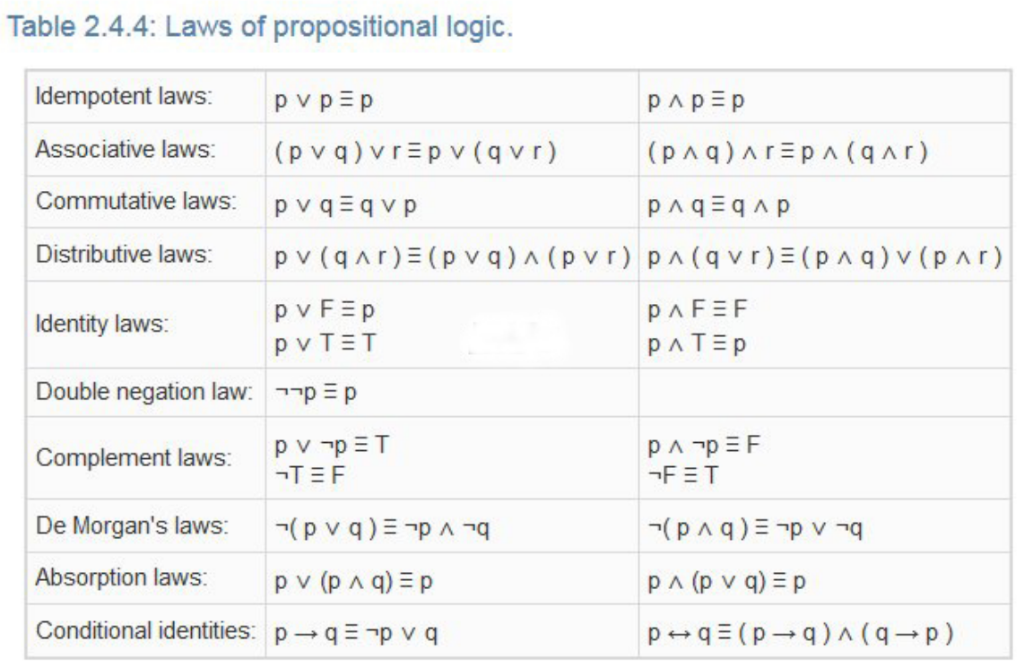
Writing the Dual
- Swap the T/F
- Replace and & or
Converse, Inverse, Contrapositive
Statement: p->q
Contrapositive: ~Q->~P (logical equivalence)
Inverse: ~P->~Q
Converse: Q->P (logical equivalence)
Rules of Inference

Quantifiers
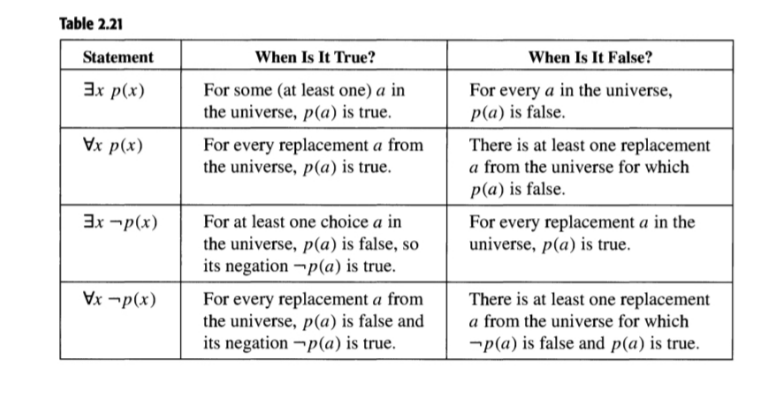
∀: For all
∃: There exists
- ∀X ∃Y f(x, y) means for all x there exists one y.
- ∃X ∀Y f(x, y) means that there exists an X for all y.
When writing contrapositive, converse, inverse we keep the quantifiers the same.
Negating Quantifiers

We start by adding the ~ in front of the whole statement then we distribute by steps.
So first distribute the not to the quantifier so that it changes to the other quantifier. Then put the ~ in front of the rest of the statement and distribute accordingly.
Rules of Inference For Quantifiers
Universal instantiation:
Universal generalization:
Proofs of Theormes
Direct proof: assume p and show q is true.
Indirect proof: